Di Posting Oleh : INFO PENDIDIKAN
Kategori : EDUCATION Integral
Materi: Integral Tak Tentu Soal & Pembahasan - Jumpa lagi teman di blog saya, pada kesempatan kali ini aku akan membahas bahan matematika yaitu integral. Pada dasarnya, integral merupakan kebalikan dari turunan / differensial. Maka integral sering disebut sebagai anti differensial.
Kegunaan integral dalam kehidupan sehari-hari amatlah banyak, menyerupai memilih luas suatu bidang, memilih volume benda putar, memilih panjang bujur, dll. Integral dibagi menjadi dua macam, yaitu integral tak tentu dan integral tentu. Nah, kali ini aku akan membahas perihal integral tak tentu terlebih dahulu. Mari teman pribadi saja.
Pengertian integral tak tentu --> integral yang nilainya tak tentu. Karena integral merupakan kebalikan (invers) dari turunan maka untuk memilih rumusnya kita beranjat terlebih daluhu ke turunan. Dari analisa tersebut didapat rumus integralnya :
Rumus-rumus Integral Tak Tentu
1. ∫ a dx = ax + c
2. ∫ a f(x) dx = a ∫ f(x) dx
Contoh Soal :Tentukan hasil integral fungsi-fungsi berikut... 1. ∫ 6 dx = .... 2. ∫ 8x5 dx = .... 3. ∫ 2 3√x = .... 4. ∫ (x + 3)2 = ....Pembahasan :
1. ∫ 6 dx = 6x + c 2. ∫ 8x5 dx = 8 ∫ x5 dx = 8/5+1 (x5+1) + c = 8/6 (x6) + c = 4/3 x6 + c 3. ∫ 2 3√x = 2/ ⅓+1 (x⅓+1) + c = 6/4 x4/3 + c = 3/2 x4/3 + c 4. ∫ (x + 3)2 = ∫ (x2 + 6x + 9) dx = ⅓x3 + 3x2 + 9x + cMungkin itu saja info yang sanggup aku berikan tentang Materi: Integral Tak Tentu Soal & Pembahasan supaya bermanfaat.
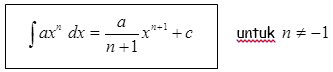
0 Response to "Info Pendidikan - Materi: Integral Tak Tentu Soal & Pembahasan"